Topics from the Cambridge IGCSE (9-1) Computer Science syllabus.

DATA REPRESENTATION - 1.2.2 | SOUND REPRESENTATION

Topics from the Cambridge IGCSE (9-1) Computer Science 0984 syllabus 2023 - 2025.

OBJECTIVES
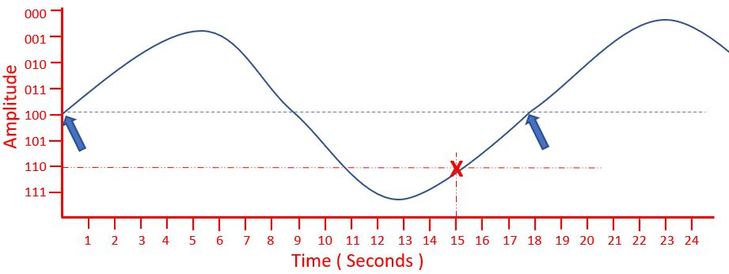
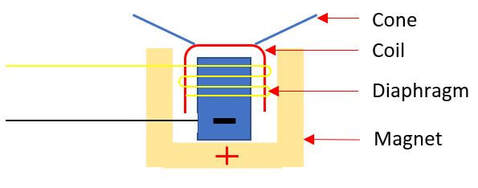
1.2.2 Understand how and why a computer represents sound, including the effects of the sample rate and sample resolution

LEARN
TERMINOLOGY
QUESTIONS
FLASHCARDS
WORKBOOK

Hello! Today, we’re diving into how computers represent sound. Sound is created by vibrations that oscillate in wave forms, creating changes in air pressure. Each of these waves has a frequency, which is the number of oscillations per second, measured in hertz. In its natural form, sound travels as an analog wave. However, to work with sound on a computer, we need to convert this analog wave into a digital format that a computer can process. This is done by taking snapshots, or samples, of the wave at regular intervals. Key Factors in Sound Sampling There are two main factors to consider when converting sound into digital form: Sample Rate The sample rate is the number of samples taken per second. Higher sample rates capture more details of the original sound wave, making the digital recording more accurate. For example, if we take 40,000 samples per second, we’re capturing a high level of detail. Sample Resolution or Bit Depth The sample resolution, also known as bit depth, represents the number of points on the wave’s amplitude that we can capture. A higher bit depth allows for a more accurate representation of sound volume and quality. In the diagram, if we were to take two samples per second, we’d capture only 36 samples in one wave oscillation. This limited sample rate might miss details. In practice, however, sample rates are much higher – often around 40,000 samples per second – and bit depth is typically 16 or 32 bits for better sound quality. Nyquist’s Theorem and the Scope of Human Hearing To get an accurate digital representation of a sound wave, Nyquist’s theorem tells us to sample at least twice the frequency of the highest sound in the original wave. This means if a sound wave has a frequency of 10,000 hertz, we’d need a sample rate of at least 20,000 samples per second to capture it accurately. Also, consider that the human ear can only hear sounds between 20 hertz and 20,000 hertz. Many sounds outside this range don’t need to be recorded, so audio processing often uses a band-limiting filter to clip these frequencies. Choosing the Right Sample Rate and Bit Depth The right sample rate and bit depth depend on the purpose and quality of the recording. For high-quality recordings intended for professional sound systems, a high sample rate and bit depth are necessary. For online streaming, like on YouTube, a lower sample rate and bit depth can reduce file size and allow for faster streaming. Calculating Sound File Size To calculate the size of a sound file, we use this formula: File Size = Sample Rate × Bit Depth × Time (in seconds) For example, if we record at a sample rate of 10,000 samples per second with a 16-bit depth over 60 seconds, the file size is 9,600,000 bits. In summary, computers represent sound by capturing samples of the analog wave at a certain rate and resolution. By understanding sample rate, bit depth, and file size calculations, we can ensure high-quality digital sound or optimize file size for various uses.

Read Aloud

■

WHAT IS SOUND ?

Sound is vibrations that oscillate in wave forms creating a change in pressure. Each wave is defined as a frequency, one oscillation can be seen in the diagram below.

Showing one full oscillation and a frequency of 18 Hertz

Frequency is measured in hertz. The diagram above shows one complete oscillation in 18 seconds, this means the wave have a frequency of 18 hertz.

Sound travels as an analogue wave and we need to convert the analogue wave into digital representation for computer use. When converting the analogue wave into digital format there are two main factors we need to consider.

How often do we want to take a sample of the original sound wave(times per second), this is known as sample rate.
At what points on the amplitude do we want to take a sample, the amount of points on the amplitude that we are able to take a sample is called the bit depth or resolution.

If we were looking to convert the above sound wave into digital, we can only take samples were the wave meets a bit depth point and we can only take samples on a predefined time per second. If we were to take 2 samples per second then we would have taken 36 samples of the one oscillation illustrated. These samples can only be recorded on one of the bit depth levels. As illustrated with the sample taken at 15 seconds (marked X).

The above diagram has a bit depth of 3, because 3 bits have been used to represent the amplitude, this would mean a maximum of 8 or 2^3 points on the amplitude could be digitally represented.

Note: The values used are just for illustration purpose, in practice you could expect a sample rate of about 40,000 and a bit depth of 32.

When considering what sample rate and what bit depth to use there are a few factors to influence this decision.

Nyquist's theorem - We need to sample a sound wave at double its highest frequency to be able to produce an accurate reproduction of the original.
The scope of the human ear - The human ear can hear between 20Hz and 20,000Hz, much of a sound wave will be out of this range and not worth recording anyway. A band-limiting filter if often used to clip frequency out of the 20Hz - 20,000Hz range.
The purpose of the recording and the medium through which it is used. - If the sound expected to be high quality and is to be played on a high quality sound system then a high sample rate and high bit depth is needed. If less quality is needed of it is to be streamed to platforms like youtube then a lower sample rate and bit depth would allow for faster data transfer.

According to Nyquist's theorem if a sound wave has a frequency of 10,000Hz we would need to sample at 20,000 samples per second to get an accurate reproduction of the original. Most CDs are recorded at 44,100 samples.

CALCULATING SOUND FILE SIZE

Samples per second x bits per second x time (in seconds)
or
Sample Rate X Bit Depth X Time
or for example
10,000(samples per second) X 16 (bit depth) X 60 (seconds) = 9,600,000 BITS

The result for the example above is shown in Bits but, it would be more appropriate to show the results in bytes, megabytes. To convert to a more appropriate representation, firstly you would divide by 8 to see how many bytes and then by 1024 for Kb and 1024 for Mb and so on..

9,600,000 / 8 = 1,200,000 Bytes
1,200,000 / 1024 = 1171.875 Kilo Bytes
1171.875 / 1024 = 1.14 Mega Bytes

1.4Mb is a much more appropriate term to use for the representation of the file size example above.

The above example presumes that the audio output is mono (the exact same sound is being sent to each speaker. Currently sound representation is at very least recorded in stereo, meaning that the left and right speaker work independently, if the sound is stored in stereo then the file size should be double. With larger home audio system a 5.1 representation could be expected, in this care each speaker has its independent sound track, Front Left, Front Center, Front Right, Rear Left, Rear Right and separate base speaker (subwoofer), in this case 6 channels may be needed so the file size could be 1.14Mb X 6. ( Check out the beach scene in 5.1 on the movie 'Saving Private Ryan' for a cool representation of 5.1 surround).

HOW DOES A MICROPHONE WORK

Internal working of a microphone

A microphone is a relative simple piece of technology using a transducer to convert movement to digital representation. It is like an inverted speaker, it uses a diaphragm to collect the sound, the diaphragm moves as waves of sound displace its position. It is delicately balanced to return to it neutral position after a sound wave has forced it to move. The diaphragm movement is connected a coil placed over a magnet this movement creates an electrical charge, as it movements alternates the electric current flowing alternates. This value can then be measured and converted into a digital representation of sound by measuring the frequency and depth of change.

Click here to check out how a microphone works

CHECK YOUR KNOWLEDGE

What does a higher sample rate in digital audio recording achieve?

A) It increases the volume of the recorded audio.

B) It captures more details of the sound wave, resulting in higher quality.

C) It reduces the size of the audio file.

D) It reduces the amount of memory needed to store the audio.

EXPLAINATION

The correct answer is B: "It captures more details of the sound wave, resulting in higher quality." A higher sample rate increases the number of samples per second, which captures more detail from the original sound wave, leading to better sound quality.

Sound Representation | The process by which a computer stores and interprets sound data in binary form.
Digital Audio | Audio that has been converted from an analog sound wave into a digital format using binary numbers.
Sample Rate | The number of samples taken per second when converting analog sound into digital form, measured in hertz (Hz). Higher sample rates capture more detail.
Sample Resolution | Also known as bit depth, it refers to the number of bits used to represent each audio sample. Higher sample resolution allows for more precise representation of sound.
Bit Depth | The number of bits in each audio sample. Common bit depths include 8-bit, 16-bit, and 24-bit, with higher values allowing for greater dynamic range in sound.
Hertz (Hz) | The unit of frequency, representing cycles per second. In audio, sample rate is often measured in hertz, such as 44,100 Hz (44.1 kHz).
Analog to Digital Conversion (ADC) | The process of converting continuous analog sound waves into discrete digital samples that a computer can process.
Amplitude | The height of a sound wave, representing the volume or loudness. Higher amplitudes correspond to louder sounds and are represented by higher numerical values in digital audio.
Dynamic Range | The range between the softest and loudest parts of a sound, measured in decibels (dB). Higher bit depths in digital audio capture a greater dynamic range.
Decibel (dB) | A unit used to measure the intensity or loudness of sound. In digital audio, higher bit depths support a wider dynamic range in decibels.
Compression (Audio) | Techniques used to reduce the file size of digital audio. Lossy compression reduces file size by discarding some data, while lossless compression retains all original data.
Quantization | The process of mapping a large set of values (such as a range of sound amplitudes) to a smaller set, based on the sample resolution. Quantization can lead to slight inaccuracies known as quantization error.
Quantization Error | Small differences between the actual amplitude of the analog sound wave and its digital representation due to rounding in quantization.
Frequency | The rate at which a sound wave oscillates, measured in hertz (Hz). In digital audio, the sample rate must be at least twice the highest frequency to accurately reproduce the sound.
Nyquist Theorem | A principle stating that the sample rate must be at least twice the highest frequency present in the sound to avoid distortion and accurately reproduce it.

1: Fill in the blanks
A microphone captures sound in an analogue format, before the computer can represent this a .............................. is needed to convert the sound to a .................... format.
2: Describe what is meant by the term 'sampling'.
3: Explain why the sample rate effects the quality of the sound
4: Describe what is meant by the term 'bit depth'.
5: Describe what is meant by the term 'channel'.
6: Sound for youtube videos is often not represented at high quality, give 3 reasons why this might be the case for this scenario.

SOUND FILE SIZE

1: Calculate the file size for the following sound sample, give the size in MB

Mono
Sample rate: 42000
Bit Depth: 16bit
Time: 60 seconds

2: Calculate the file size for the following sound sample, give the size in MB

Stereo
Sample rate: 20000
Bit Depth: 16bit
Time: 120 seconds

3: What happens to the file size as more channels are represented?

4: Calculate the file size for the following sound sample, give the size in MB

4 channel
Sample rate: 44100
Bit Depth: 16
Time: 180