Topics from the Cambridge IGCSE (9-1) Computer Science syllabus.

1.1.6 | TWO'S COMPLEMENT

Topics from the Cambridge IGCSE (9-1) Computer Science 0984 syllabus 2023 - 2025.

OBJECTIVES
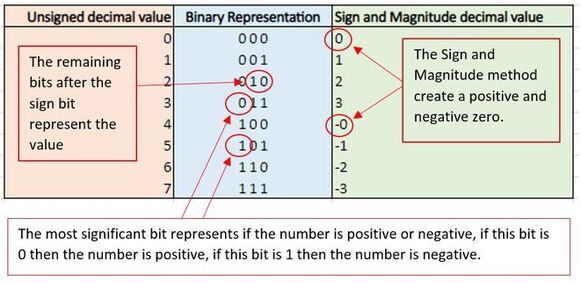
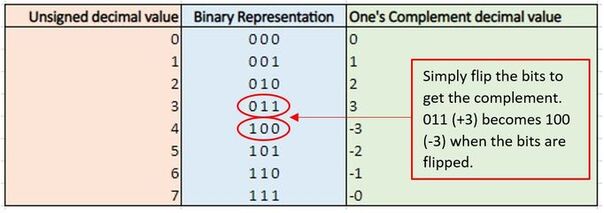
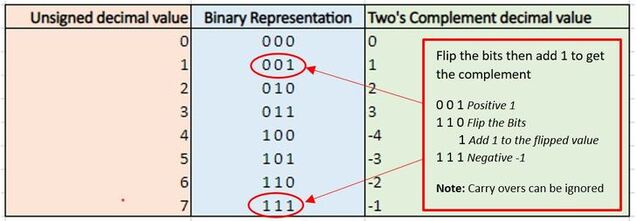
1.1.6 Use two’s complement to represent positive and negative 8-bit binary integers

Convert a positive binary or denary integer to a two’s complement 8-bit integer and vice versa
Convert a negative binary or denary integer to a two’s complement 8-bit integer and vice versa

ALSO IN THIS TOPIC
1.1.1 NUMBER SYSTEMS
1.1.2 NUMBER SYSTEMS
1.1.3 NUMBER SYSTEMS
1.1.4 NUMBER SYSTEMS
1.1.5 NUMBER SYSTEMS
YOU ARE HERE | 1.1.6 NUMBER SYSTEMS
1.2.1 TEXT, SOUND AND IMAGES
1.2.2 TEXT, SOUND AND IMAGES
1.2.3 TEXT, SOUND AND IMAGES
1.3.1 STORAGE AND COMPRESSION
1.3.2 STORAGE AND COMPRESSION
1.3.3 STORAGE AND COMPRESSION
1.3.4 STORAGE AND COMPRESSION
TOPIC 1 KEY TERMINOLOGY
TOPIC 1 ANSWERS
TOPIC 1 TEACHER RESOURCES (CIE)

WHAT IS NEGATIVE NUMBER REPRESENTATION ?

Computers use various methods of representing negative numbers. The three methods of representing negative numbers discussed here are:

Sign and Magnitude
One's Complement
Two's Complement

A normal binary number that has had no change made to it would be referred to as 'unsigned binary' , so if an exam question gives a binary number and stipulates that it is unsigned then it is a simple straight forward binary number. (As was represented on the binary page of this website), for example:

0 1 0 1 1 0 0 1 represents the numeric value of 89

SIGN AND MAGNITUDE
Sign and magnitude is a simple method of representing negative. It simply takes the most significant BIT (the left hand bit) of a binary value and uses it to represent if the number is positive or negative.

The rule of Sign and Magnitude is:

The most significant bit represents if it is positive or negative(0 = positive, 1 = negative)
The remaining bits represent the value of the number

As can be seen in the table below.

Sign and Magnitude works but it is not a very good method of representing negative numbers because:

It creates two 0s : A positive 0 and a negative 0
It creates hardware problems in the processing of these numbers

If you have an exam question that say the number given is already in Sign and Magnitude representation then you need to answer accordingly.

Question: If 10001101 is already in its Sign and Magnitude representation then what would the denary value be?
Answer: -13 :Because the most significant bit is 1 so we know it is a negative number and then the remaining bits add up to 13 therefore the answer is negative -13.

ONES COMPLEMENT

One's complement is another method of representing negative numbers. Computer hardware can process One's Complement numbers better than those represented in Sign and Magnitude however, one's complement still produces two 0s.

The rule of One's complement is:

Take the positive value and flip the bits to create the complement.

So for example, take 0 0 1 which represents the denary value of 1, flip the bits (change the 0s to 1s and 1s to 0s), this gives you 1 1 0 which in One's Complement represents negative -1 . Again the positive values will always be represented with 0 being the most significant bit.
As can be seen in the table below.

One's complement is still inefficient because:

It creates two 0s : a positive 0 and a negative 0

If you have an exam question that say the number given is already in One's Complement representation then you need to answer accordingly.

Question: If 10001101 is already in its One's Complement representation then what would the denary value be?
Answer: -114 :By flipping the bits back to their original value we get 01110010 which is 114 therefore -114 is the complement.

TWOS COMPLEMENT

Two's Complement is another way of representing negative numbers in binary and it is less problematic than Sign and Magnitude or One's Complement.

The rule to convert a number into its Two's complement representation are;

Flip the bits
Add 1

As can be seen in the table below, if we flip the BITs(same as in One's Complement) then add 1 to the flipped result, the answer represents the Two's complement value.

Two's complement is more efficient because:

It only produces one Zero
It does not create hardware problems in processing

If you have an exam question that say the number given is already in Two's Complement representation then you need to answer accordingly.

Question: If 10001101 is already in its Two's Complement representation then what would the denary value be?
Answer: -115 :Because (working in reverse) if we take 01110011 (115) flip the bits it gives us 10001100, add 1 to this value give us 10001101. So the answer is negative -115.

1: What is the purpose of sign and magnitude, one's complement and two's complement methods?
2: What are the rules for sign and magnitude?
3: What are the limitations for the sign and magnitude method?
4: Using sign and magnitude what is negative representation for -55? (show your workings)
5: What are the rules for one's complement?
6: What are the limitations for the one's complement?
7: Using one's complement what is negative representation for -55? (show your workings)
8: What are the rules for two's?
9: Using two's complement what is negative representation for -55? (show your workings)
10: If the value 10101000 is already in two's complement, what is the Denary value represented?

NEXT PAGE | BINARY AND HEX