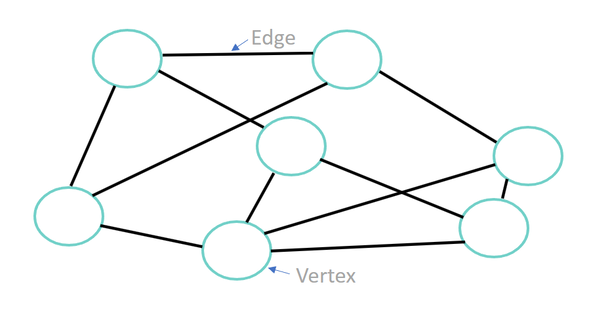
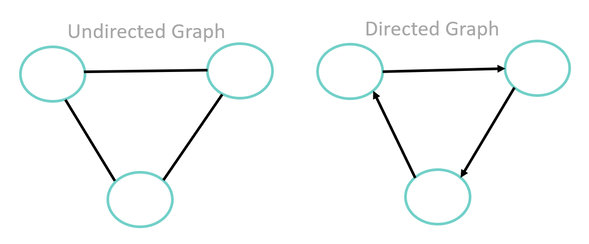
WEB SCIENCE | ANALYSING THE WEBTopics from the International Baccalaureate (IB) 2014 Computer Science Guide.
|
|
|
ON THIS PAGE
SECTION 1 | DIRECTED GRAPH REPRESENTATION SECTION 2 | WEB GRAPHS AND SUB-GRAPHS SECTION 3 | WEB GRAPH STRUCTURE SECTION 4 | GRAPH THEORY AND CONNECTIVITY SECTION 5 | SEARCH ENGINES AND WEB CRAWLING SECTION 6 | WEB DEVELOPMENT PREDICTIONS |